Алгебра 7 Мерзляк С-11 В3
Самостоятельная работа № 11 по алгебре в 7 классе «Сложение и вычитание многочленов» с ответами (Вариант 3). Дидактические материалы (упражнения №№ 76 — 91) для учителей, учащихся и родителей. Алгебра 7 Мерзляк С-11 В3.
Алгебра 7 класс (Мерзляк)
Самостоятельная работа № 11. Вариант 3
№ 76. Упростите выражение: 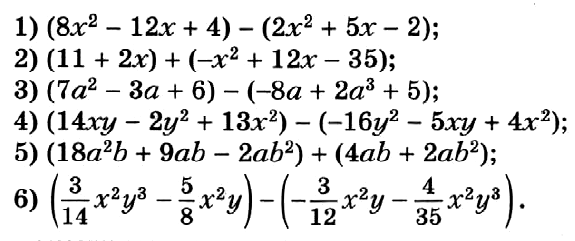 № 77. Докажите тождество:
№ 77. Докажите тождество:
1) (a2 – b2 – с2) – (b2 – с2 + a2) + (b2 – a2) = –a2 – b2;
2) –2a2 – (4 – 3a2) + (6 – 5a2) + (4a2 – 2) + 1 = 1;
3) (х3 + 5x2) – (2х – 1) – (x2 + 3х) + (5х – х3) = 4x2 + 1.
№ 78. Докажите, что значение выражения не зависит от значений переменных, входящих в него:
1) (12а5 + 2а4 + 3) – (5а5 + 4а4 – 8) – (7а5 – 2а4 – 11);
2) (3/8 • a2 – 2/9 • ab) + (ab/3 – а2/2) – (ab/9 – a2/8).
№ 79. Решите уравнение:
1) 5 – (3 + 4х – 2x2) = 2x2 – 3х + 8;
2) 12 + (5х + 3x2) – (3x2 – 2х) = 0;
3) (3у3 + 2y2 – 4) – (2у3 + 4y2 – 3у) = у3 – 2y2 – 12.
№ 80. Найдите значение выражения:
1) 4a2 – (8a2 – 2ab) + (3аb + 4a2), если а = 0,2, b = 3;
2) (5ху – x2) + 7x2 – (6x2 – 3ху), если х = –3/2, у = 1 3/4.
№ 81. Вместо звёздочки запишите такой многочлен, чтобы образовалось тождество:
1) * – (2x2 + 3ху – 4y2) = 5x2 – y2;
2) а3 – 6a2 + 2а4 – (*) = 8a2 – 3а4 + 1.
№ 82. Докажите, что выражение (9x6 – 2x3 + 1) – (х3 + х – 2) + (3x3 + х) принимает положительные значения при любых значениях х. Какое наименьшее значение принимает это выражение и при каком значении х?
№ 83. Докажите, что значение выражения (11n + 5) – (4n – 16) кратно 7 при любом натуральном значении n.
№ 84. Докажите, что значение выражения (10n – 3) – (2n – 19) кратно 8 при любом натуральном значении n.
№ 85. Докажите, что при любом натуральном n значение выражения (9n + 7) – (4n + 5) при делении на 5 даёт остаток, равный 2.
№ 86. Представьте в виде многочлена выражение: ![]()
№ 87. Докажите, что разность чисел cba и cab кратна 9.
№ 88. Докажите, что разность abc – (а – b + с) кратна 11.
№ 89. Представьте многочлен 5хy2 – 2x2 + 4х – 3у + 1 в виде суммы двух многочленов так, чтобы один из них не содержал переменной у.
№ 90. Представьте многочлен 2x2у + 3y2 – 4х4 + 7ху – 8х + 9 в виде разности двух многочленов с положительными коэффициентами.
№ 91. Представьте многочлен 2y2 + 4у – 5 в виде разности двух двучленов.
Алгебра 7 Мерзляк С-11 В3
ОТВЕТЫ на самостоятельную работу:
Вы смотрели: Самостоятельная работа по алгебре в 7 классе «Сложение и вычитание многочленов» с ответами. Дидактические материалы для учителей, учащихся и родителей.
Другие варианты: С-11. Вариант 1 С-11. Вариант 2
Вернуться к Списку самостоятельных работ по алгебре в 7 классе УМК Мерзляк.
Перейти к Списку контрольных работ по алгебре в 7 классе УМК Мерзляк.
Цитаты (упражнения) из учебного пособия «Дидактические материалы. Алгебра 7 класс / Мерзляк, Полонский, Рабинович, Якир — М.:Вентана-Граф» использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). Решения и ОТВЕТЫ на самостоятельную работу (нет в пособии) адресованы родителям для проверки знаний учащихся.

