ОТВЕТЫ на КР3 Алгебра 9 Мордкович
ОТВЕТЫ на КР3 Алгебра 9 Мордкович — это цитаты из пособия для учащихся «Контрольные и самостоятельные работы по алгебре в 9 классе», которое используется в комплекте с учебником А.Г. Мордковича «Алгебра 9 класс».
Вернуться к Списку работ (в ОГЛАВЛЕНИЕ)
Алгебра 9 класс (Мордкович)
Ответы на Контрольную № 3
Проверяемые темы учебника:
Определение числовой функции. Область определения, область значений функции. Способы задания функций. Свойства функций. Четные и нечетные функции. Функции у = хn (n ∈ N), их свойства и графики. Функции у = х–n (n ∈ N), их свойства и графики. Функция у = 3√х, ее свойства и график.
Кр-3. Вариант 1
№ 1. Постройте график функции: а) у = –2х4; б) у = 5/x3.
РЕШЕНИЕ:
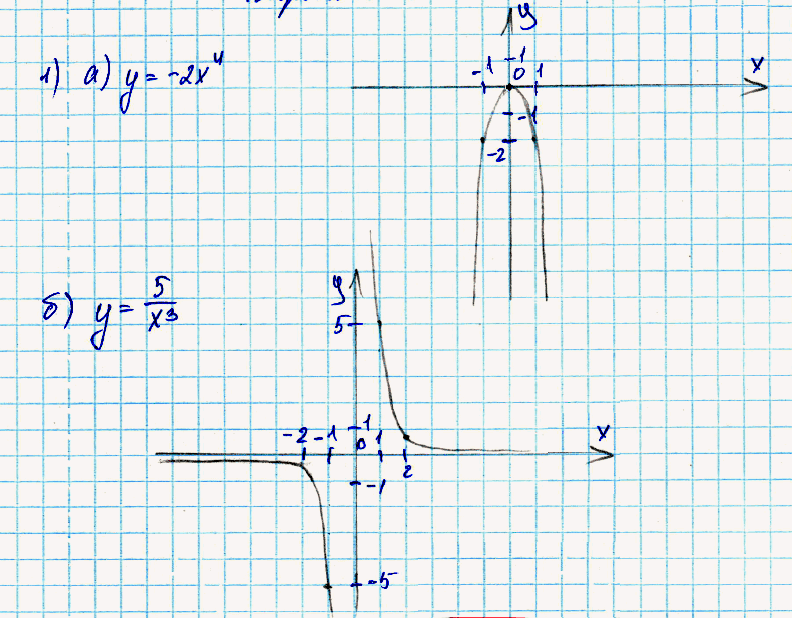
№ 2. Докажите, что функция у = 2х2 + х6 + х8 + 1 является четной.
РЕШЕНИЕ:
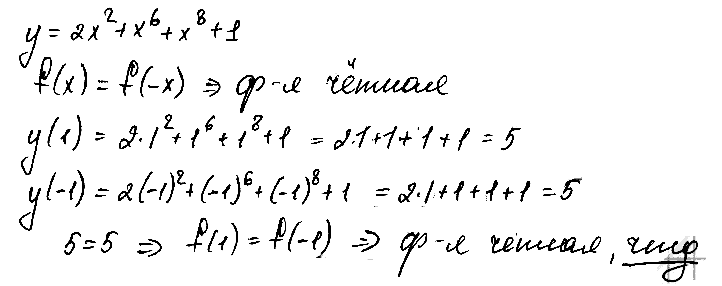
№ 3. Используя свойства числовых неравенств, докажите, что функция у = –х5 – х + 3 убывает.
РЕШЕНИЕ:
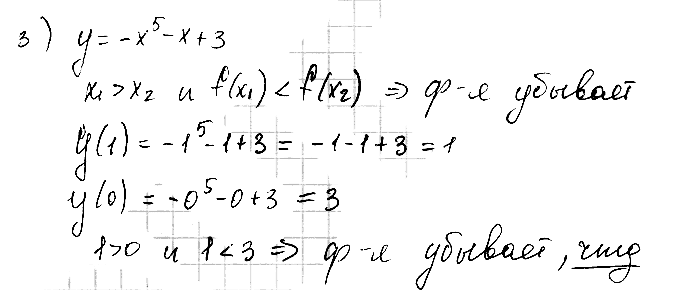
№ 4. Найдите наименьшее и наибольшее значения функции у = 3√x + x + 2, x ∈ [1; 21].
РЕШЕНИЕ:
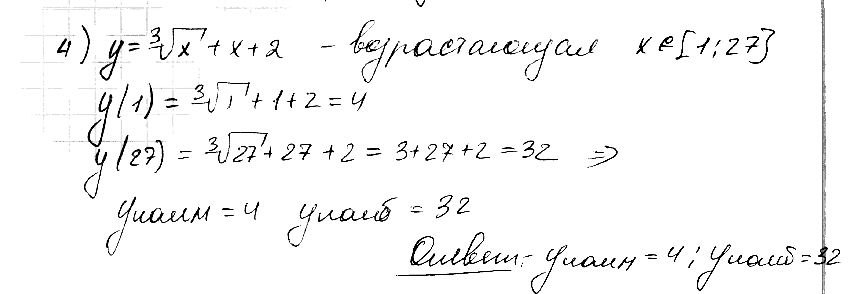
№ 5. Дана функция у = f(x), где f(х) = 1 – х4.
Докажите, что (f(–2х) – 1)2 = 256(1 – 2f(x) + f2(х)).
РЕШЕНИЕ:
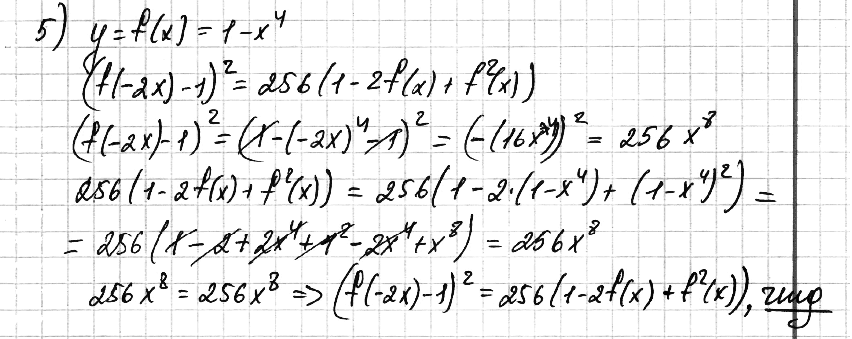
Кр-3. Вариант 2
№ 1. Постройте график функции: а) у = –3х2; б) у = 6/x4.
РЕШЕНИЕ:
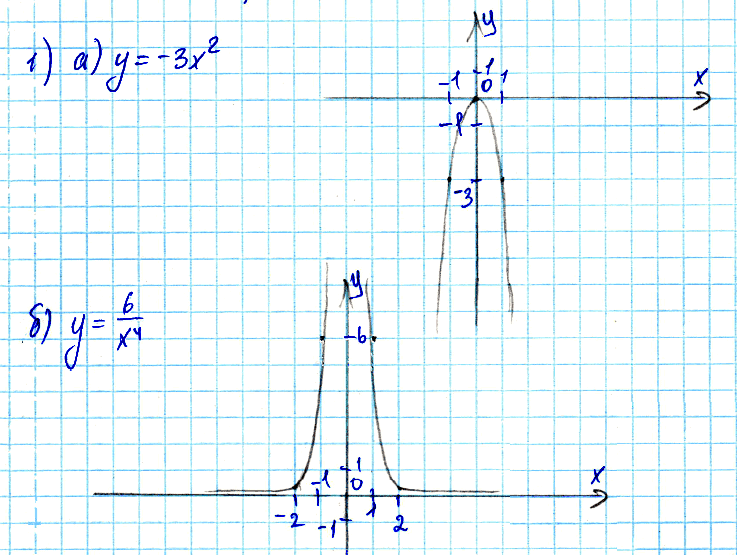
№ 2. Докажите, что функция у = 3х3 + x7 + х5 является нечетной.
РЕШЕНИЕ:
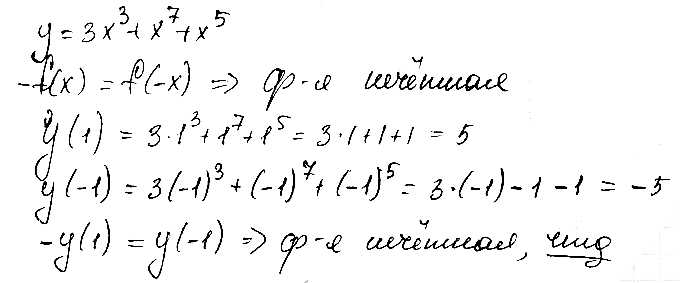
№ 3. Используя свойства числовых неравенств, докажите, что функция у = 2х3 + 5х возрастает.
РЕШЕНИЕ:
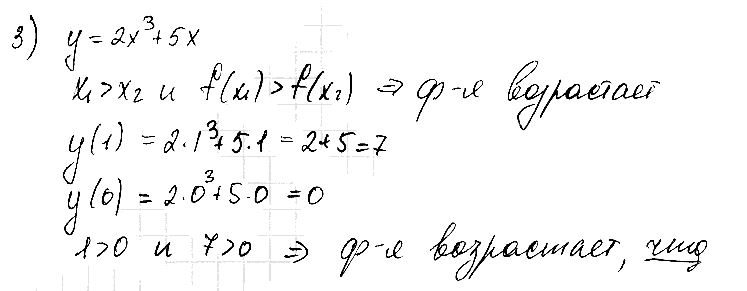
№ 4. Найдите наименьшее и наибольшее значения функции у = √x + х2 – 1, х ∈ [4; 5].
РЕШЕНИЕ:

№ 5. Дана функция у = f(х), где f(х) = х3 + 1.
Докажите, что (f(–х) – 1)3 = –(f(х) – 1)3.
РЕШЕНИЕ:
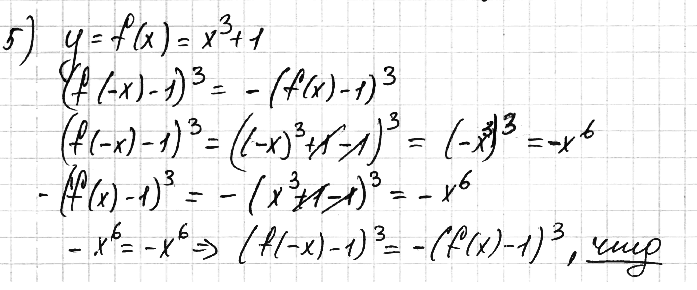
Вы смотрели: ОТВЕТЫ на КР1 Алгебра 9 Мордкович — «Контрольные и самостоятельные работы по алгебре в 9 классе», которое используется в комплекте с учебником А.Г. Мордковича «Алгебра 9 класс».
Вернуться в Оглавление (список контрольных по алгебре в 9 классе)
