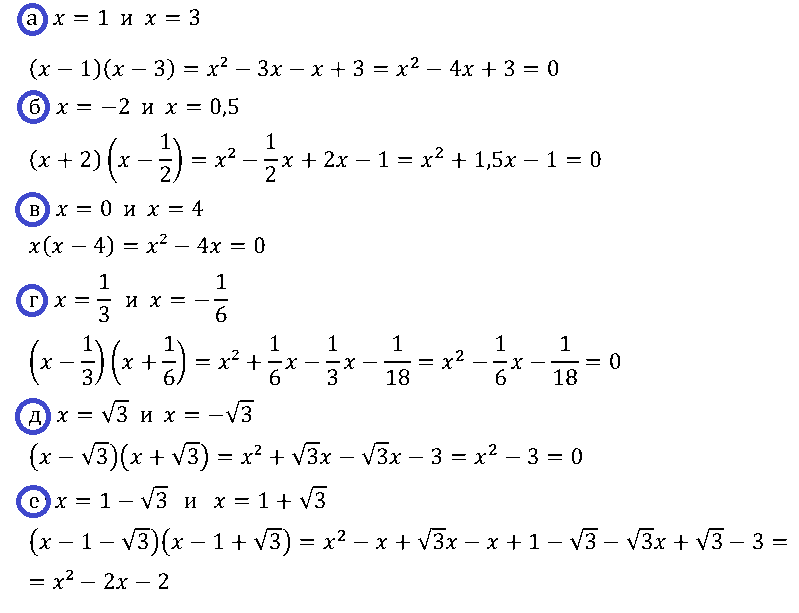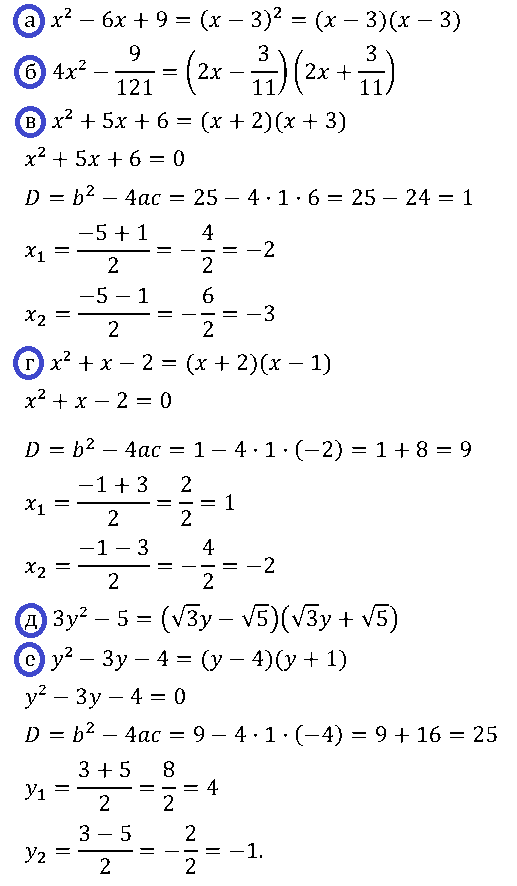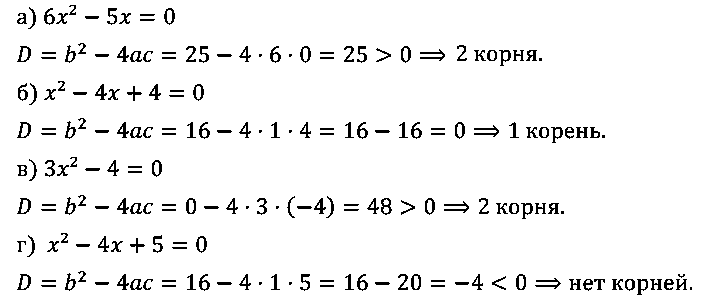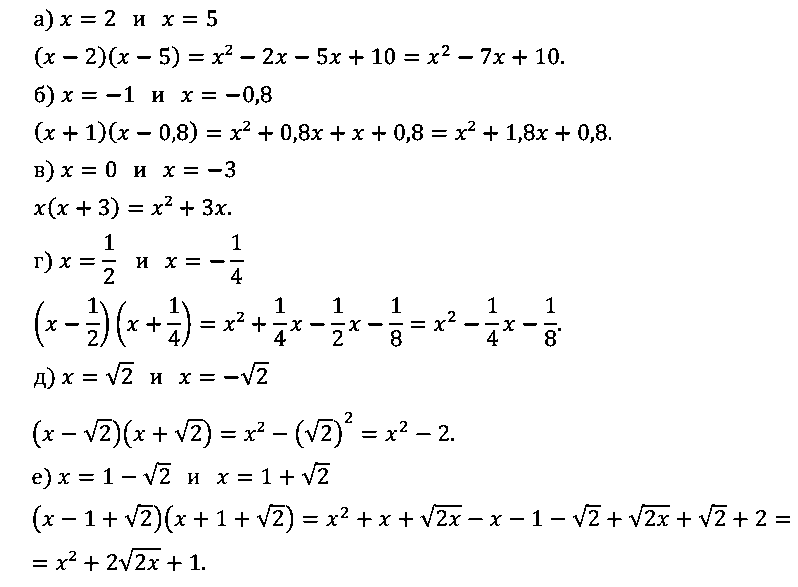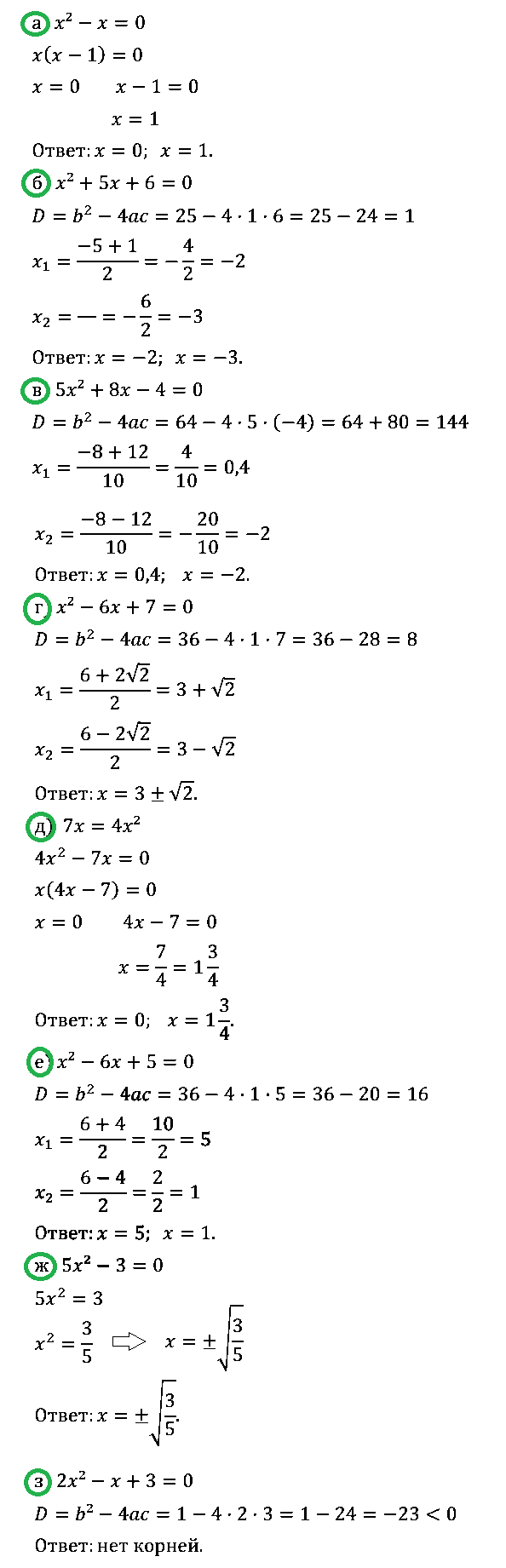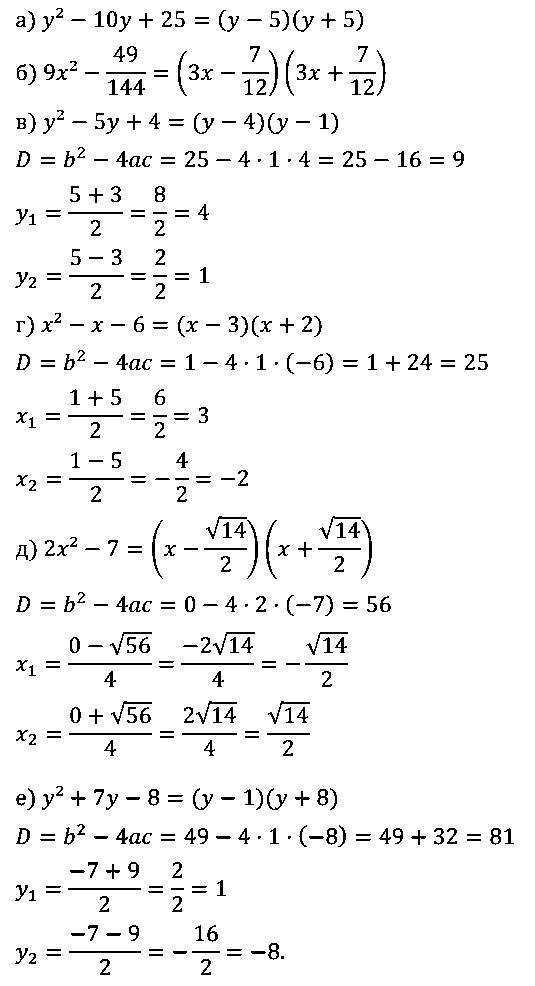Алгебра 8 Макарычев Самостоятельная С-25
Самостоятельная работа по алгебре в 8 классе с решениями и ОТВЕТАМИ для УМК Макарычева по теме «Решение квадратных уравнений». Цитаты из пособия указаны в учебных целях. Алгебра 8 Макарычев Самостоятельная С-25 + решения.
Вернуться к Списку самостоятельных работ (в ОГЛАВЛЕНИЕ)
Самостоятельная работа № 25
Алгебра 8 класс (УМК Макарычев)
C-25. Вариант 1 (задания и ответы)
№ 1. Какие из чисел 0; 1/3; –1; –0,5; 2 являются корнями уравнения:
а) x2 – х – 2 = 0; б) 2x2 + х = 0; в) 2x2 – 3х – 2 = 0; г) 3x2 + 2х – 1 = 0?
№ 2. Найдите дискриминант квадратного уравнения:
а) 3x2 – 5х + 2 = 0; б) 4x2 – 4х + 1 = 0; в) 2х – x2 + 3 = 0; г) 3х – 1 + 6x2 = 0.
ОТВЕТ:
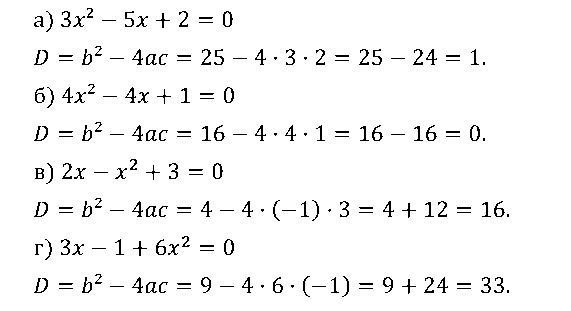
№ 3. Сколько корней имеет уравнение:
а) 3x2 – 7х = 0; б) x2 – 2х + 1 = 0; в) 2x2 – 1 = 0; г) x2 + 3х + 3 = 0?
№ 4. Составьте квадратное уравнение, корни которого равны:
а) 1 и 3; в) 0 и 4; д) √3 и –√3;
б) –2 и 0,5; г) 1/3 и –1/6; е) 1 – √3 и 1 + √3.
№ 5. При каких значениях n можно представить в виде квадрата двучлена выражение:
а) x2 – nх + 16; б) x2 + 6х – n; в) nx2 – 12х + 4; г) x2 + nх + 4/49?
ОТВЕТ:
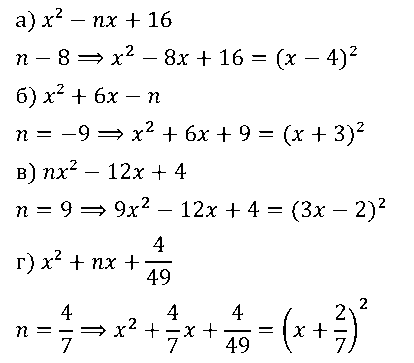
№ 6. Решите уравнение:
а) x2 + х = 0; б) x2 – 4х + 3 = 0; в) 5x2+ 14х – 3 = 0; г) x2 – 2х – 2 = 0;
д) 5х = 3x2; е) x2 – 5х + 4 = 0; ж) 7x2 – 4 = 0; з) 3x2 – х + 2 = 0.
№ 7. Найдите корни уравнения:
а) 10x2 + 5х – 0,6 = 0; б) 7x2 + 8х + 1 = 0; в) 2x2 – 3х + 2 = 0;
г) x2 + 6 = 5х; д) 5y2 – 4y = 1; е) 2 – 3х = 5x2.
№ 8. Разложите на множители многочлен:
а) x2 – 6х + 9; б) 4x2 – 9/121; в) x2 + 5х + 6;
г) x2 + х – 2; д) 3y2 – 5; е) y2 – Зy – 4.
№ 9. При каком значении а уравнение: а) x2 – ах + 9 = 0; б) x2 + 3ах + а = 0 имеет один корень?
ОТВЕТ:
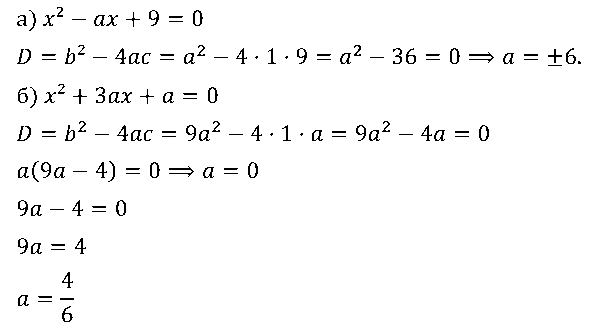
№ 10. При каком значении m один из корней уравнения 3x2 – mх – 6 = 0 равен –2?
ОТВЕТ: m = -3.
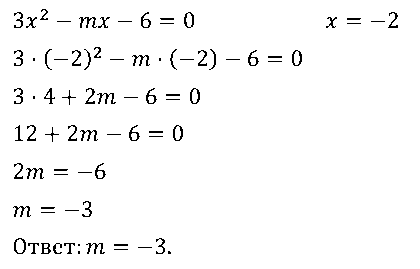
Алгебра 8 Макарычев Самостоятельная С-25
C-25. Вариант 2 (задания и ответы)
№ 1. Какие из чисел 0; 0,5; 1; –1/6; –3 являются корнями уравнения:
а) x2 + 2х – 3 = 0; б) 6x2 + х = 0; в) 2x2 + 5х – 3 = 0; г) 6x2 – 5х – 1 = 0?
№ 2. Найдите дискриминант квадратного уравнения:
а) 5x2 – 4х – 1 = 0; б) x2 – 6х + 9 = 0; в) 3х – x2 + 10 = 0; г) 2х + 3 + 2x2 = 0.
ОТВЕТ:
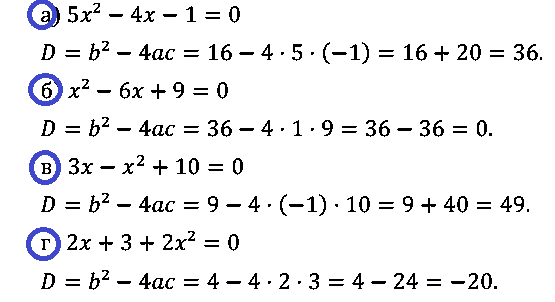
№ 3. Сколько корней имеет уравнение:
а) 6x2 – 5х = 0; б) x2 – 4х + 4 = 0; в) 3x2– 4 = 0; г) x2 – 4х + 5 = 0?
№ 4. Составьте квадратное уравнение, корни которого равны:
а) 2 и 5; г) 1/2 и –1/4;
б) –1 и 0,8; д) √2 и –√2;
в) 0 и –3; е) 1 – √2 и 1 + √2.
№ 5. При каких значениях m можно представить в виде квадрата двучлена выражение:
а) x2 + mх + 9; б) x2 – 2х – m; в) mx2 – 12х + 9; г) x2 – 2/7 • х + m?
ОТВЕТ:
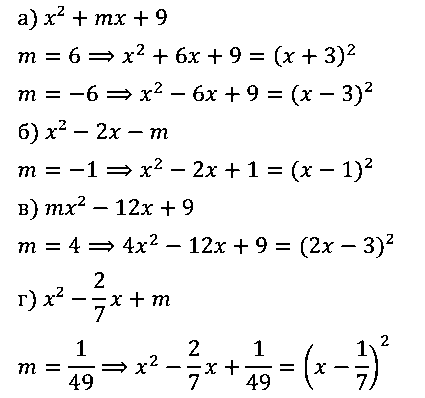
№ 6. Решите уравнение:
а) x2 – х = 0; б) x2 + 5х + 6 = 0; в) 5x2 + 8х – 4 = 0; г) x2 – 6х + 7 = 0;
д) 7х = 4x2; е) x2 – 6х + 5 = 0; ж) 5x2 – 3 = 0; з) 2x2 – х + 3 = 0.
№ 7. Найдите корни уравнения:
а) 10x2 – 3х – 0,4 = 0; б) 7x2 + 6х – 1 = 0; в) 3x2 – 4х + 2 = 0;
г) x2 + 12 = 7х; д) 7y2 + 5у = 2; е) 1 + 8х = 9x2.
№ 8. Разложите на множители многочлен:
а) y2 – 10у + 25; б) 9х2 – 49/144; в) y2 – 5у + 4;
г) x2 – х – 6; д) 2x2 – 7; е) y2 + 7у – 8.
№ 9. При каком значении а уравнение: а) x2 + ах+ 16 = 0; б) x2 – 2ах + 3а = 0 имеет один корень?
ОТВЕТЫ:
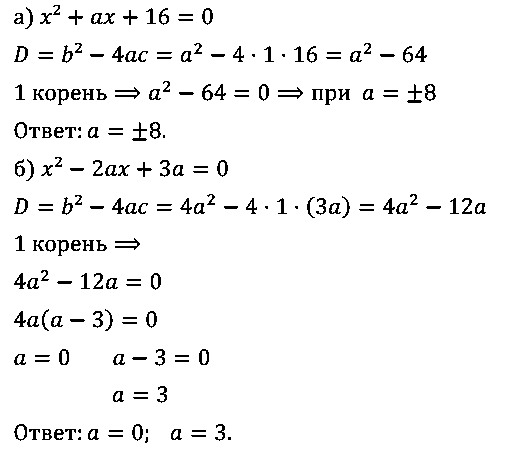
№ 10. При каком значении m один из корней уравнения 2x2 – х – m = 0 равен –3?
ОТВЕТ: m = 21.
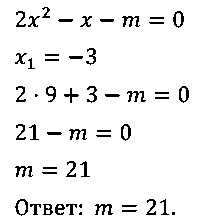
Самостоятельная работа по алгебре в 8 классе с решениями и ОТВЕТАМИ по учебнику Макарычева. Алгебра 8 Макарычев Самостоятельная С-25 «Решение квадратных уравнений». Цитаты из пособия для учащихся «Алгебра 8 класс. Дидактические материалы / Жохов, Макарычев, Миндюк — М.: Просвещение». Ознакомительная версия перед покупкой. Цитаты из пособия указаны в учебных целях.
Вернуться к Списку самостоятельных работ (в ОГЛАВЛЕНИЕ)