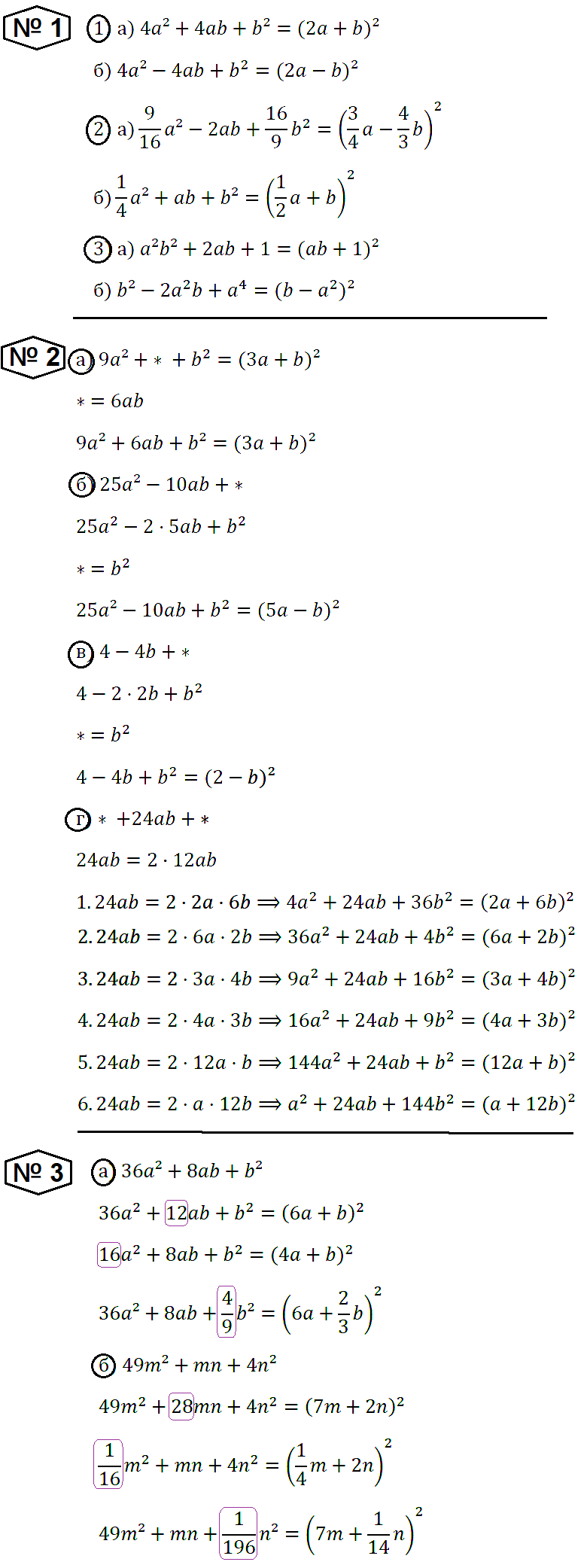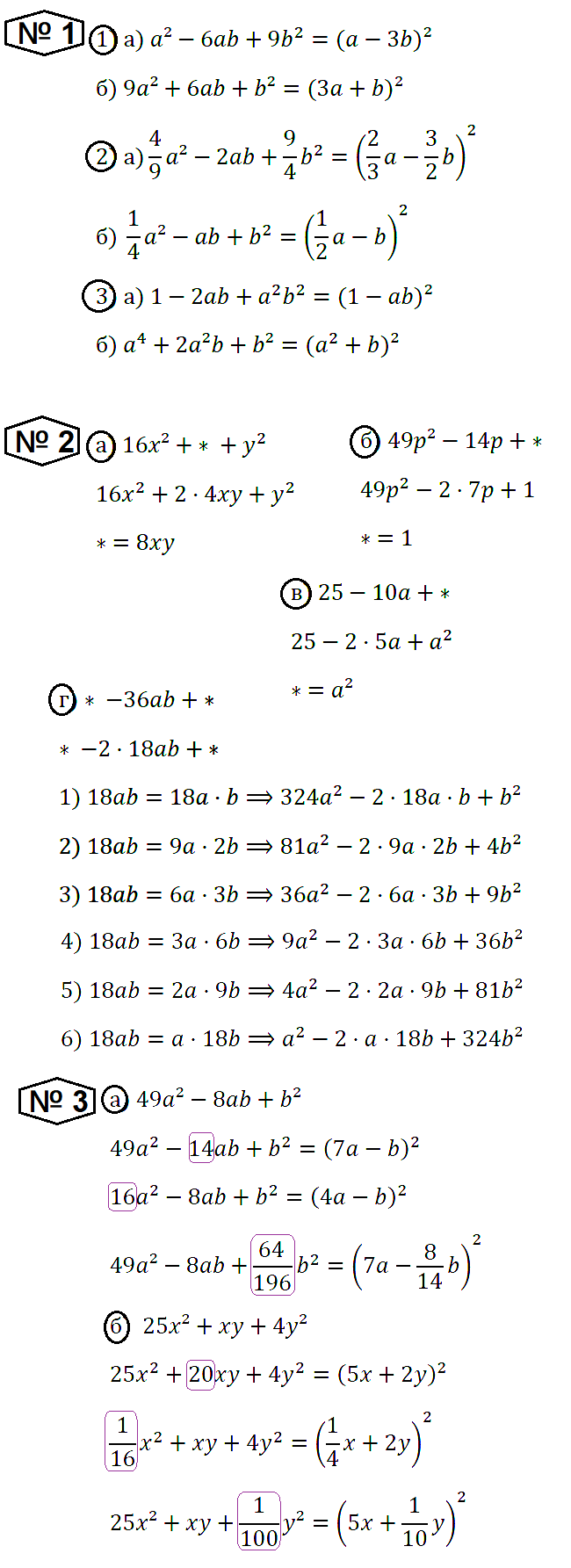Алгебра 7 Макарычев С-39

11.03.202115.02.2022 admin

Самостоятельная работа № 39 по алгебре в 7 классе «Разложение на множители с помощью формул квадрата суммы и квадрата разности» с ответами (2 варианта). Дидактические материалы для учителей, учащихся и родителей. Алгебра 7 Макарычев С-39. Ответы на самостоятельную работу адресованы родителям для проверки знаний учащихся, а также для самопроверки при дистанционном обучении.

Алгебра 7 класс (Макарычев)
Самостоятельная работа № 39

С-39 Вариант 1 (транскрипт заданий)

№ 1. Представьте многочлен в виде квадрата двучлена:
1) а) 4a² + 4аb + b²;   б) 4a² – 4аb + b²;
2) a) 9/16 • a²– 2ab + 16/9 • b²;   б) 1/4 • a² + ab + b²;
3) а) а²b² + 2аb + 1;   б) b² – 2a²b + а⁴.

№ 2. Замените значок * одночленом так, чтобы получившийся трёхчлен можно было представить в виде квадрата двучлена (задание выполните разными способами):
а) 9a² + * + b²; б) 25a² – 10ab + *; в) 4 – 4b + *; г) * + 24ab + *.

№ 3. В данном выражении измените один из коэффициентов так, чтобы получившийся трёхчлен можно было представить в виде квадрата двучлена (см. пример): а) 36a² + 8ab + b²; б) 49m² + mn + 4n².

Пример. Дано выражение 25a² + 6аb + b².
Изменив один из коэффициентов, будем иметь:
[9]a² + 6аb + b² = (3а + b)²,
или 25a² + [10]аb + b² = (5а + b)²,
или 25a² + 6ab + [9/25]b² = (5а + 3/5 • b)².

С-39 Вариант 2 (транскрипт заданий)

№ 1. Представьте в виде квадрата двучлена:
1) a) a²– 6ab + 9b²;   б) 9a² + 6ab + b²;
2) a) 4/9 • a²– 2ab + 9/4 • b²;   б) 1/4 • a²– ab + b²;
3) а) 1 – 2ab + a²b²;   б) а4 + 2a²b + b².

№ 2. Замените значок * одночленом так, чтобы получившийся трёхчлен можно было представить в виде квадрата двучлена (последнее задание попробуйте выполнить разными способами):
а) 16x² + * + y²; б) 49р² – 14р + *; в) 25 – 10а + *; г) * – 36ab + *.

№ 3. В данном выражении измените один из коэффициентов так, чтобы получившийся трёхчлен можно было представить в виде квадрата двучлена (см. пример): а) 49a² – 8аb + b²; б) 25х² + ху + 4у².

Пример. Дано выражение 9a² – 10ab + b². Изменив один из коэффициентов, будем иметь:
9a² – [6]ab + b² = (3а – b)²,
или [25]a² – 10ab + b² = (5а – b)²,
или 9a² – 10аb + [25/9]b² = (3а – 5/3 • b)².