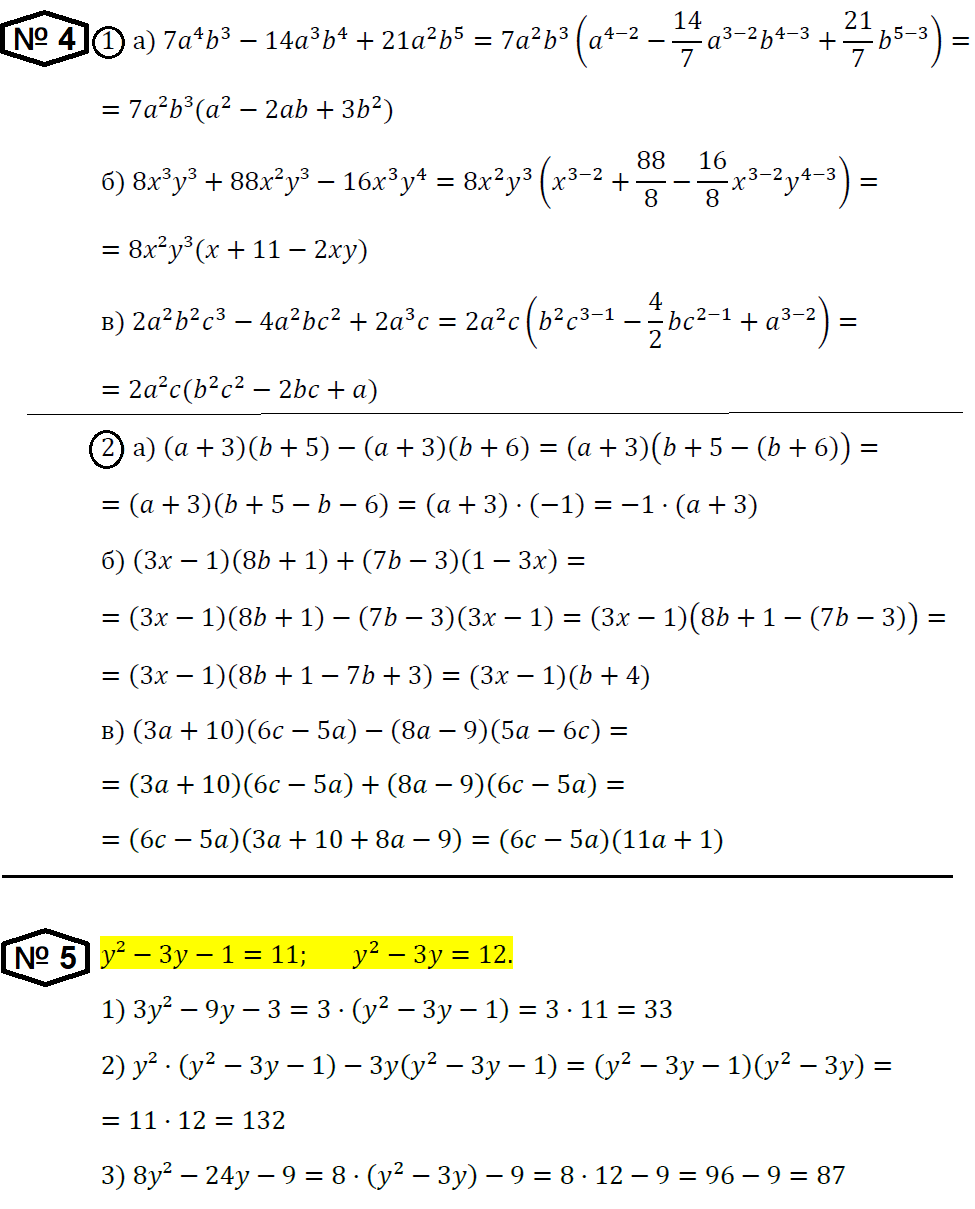Самостоятельная работа № 32 по алгебре в 7 классе «Вынесение общего множителя за скобки» с ответами (Вариант 1 ). Дидактические материалы для учителей, учащихся и родителей. Алгебра 7 Макарычев С-32 В1. Ответы на самостоятельную работу адресованы родителям для проверки знаний учащихся, а также для самопроверки при дистанционном обучении.
Алгебра 7 класс (Макарычев)Вариант 1.
С-32 В-1 (транскрипт заданий)№ 1. Вынесите общий множитель за скобки (проверьте свои действия умножением):2 ; б) 14mn2 – 7n; в) –20с2 + 80bс; г) –3а2 у – 12у2 ;4 + а3 ; б) 2z5 – 4z3 ; в) 3с6 + 7с7 – 8с8 ; г) 5х2 – 10х3 – 15х4 ;2 + 3ах; б) ху3 + 5х2 у2 – 3х2 у; в) 3а3 b – 6а2 b2 ; г) 6с2 х3 – 4с3 х2 + 2с2 х2 .
№ 2. Разложите на множители:2 (3а – 7с) – с2 (5а + 3с);
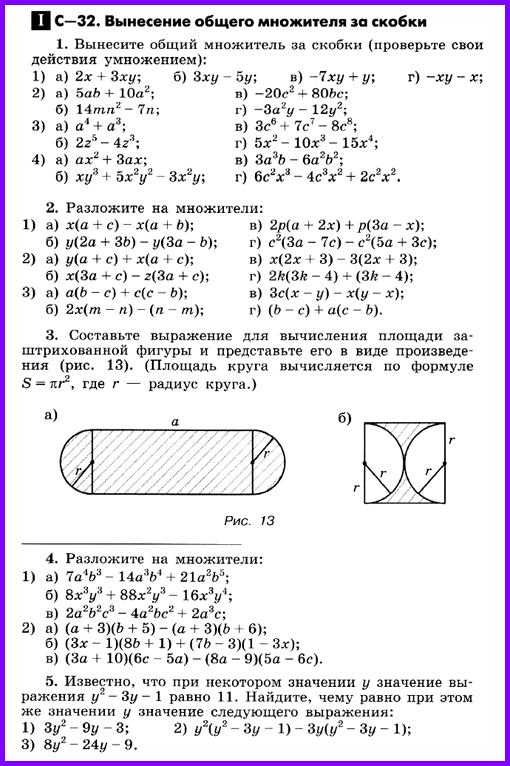
№ 3. Составьте выражение для вычисления площади заштрихованной фигуры и представьте его в виде произведения (рис. 13). (Площадь круга вычисляется по формуле S = πr2 , где r – радиус круга.)
№ 4. Разложите на множители:4 b3 – 14a3 b4 + 21а2 b5 ; б) 8х3 у3 + 88х2 у3 – 16x3 y4 ; в) 2а2 b2 с3 – 4a2 bc2 + 2а3 с;
№ 5. Известно, что при некотором значении у значение выражения у2 – 3у – 1 равно 11. Найдите, чему равно при этом же значении у значение следующего выражения:2 – 9у – 3; 2) y2 (y2 – 3у – 1) – 3y(y2 – 3y – 1); 3) 8у2 – 24у – 9.
Алгебра 7 Макарычев С-32 В1.РЕШЕНИЯ и ОТВЕТЫ: Смотреть Ответы на Вариант 1
# 1.
1) а) 2x + 3xy = x(2 + 3y). Проверка: х(2 + 3у) = 2х + 3ху => 2х + 3ху = 2х + 3ху => верно.
2) а) Проверка: 5а(b + 2а) = 5ab + 10а1+1 => 5ab + 10а2 = 5ab + 10а2 => верно.2 – 7n => 14mn2 – 7n = 14mn2 – 7n => верно.1+1 + 80bс => –20с2 + 80bс = –20с2 + 80bс => верно.2 + 4у) = –3а2 у – 12у2 => –3a2 y – 12у2 = –3a2 y – 12у2 => верно.
3) а) а4 + а3 = а3 (а4–3 + 1) = а3 (а + 1). Проверка: а3 (а + 1) = а3+1 + а3 => а4 + а3 = а4 + а3 => верно.3 (z2 – 2) = 2z5 – 4z3 => 2z5 – 4z3 = 2z5 – 4z3 => верно.6 (3 + 7с – 8с2 ) = 3с6 + 7с1+6 – 8с2+6 = 3с6 + 7с7 – 8с8 => 3с6 + 7с7 – 8с8 = 3с6 + 7с7 – 8с8 => верно.2 (1 – 2х – 3х2 ) = 5х2 – 10х2+1 – 15х2+2 = 5х2 – 10х3 – 15х4 => 5х2 – 10х3 – 15х4 = 5х2 – 10х3 – 15х4 => верно.
4) а) ах2 + 3ах = ах(х2–1 + 3) = ах(х + 3). Проверка: ах(х + 3) = ах1+1 + 3ах = ах2 + 3ах => ах2 + 3ах = ах2 + 3ах => верно.2 + 5ху – 3х) = xy2+1 + 5х1+1 у1+1 – 3х1+1 у = ху3 + 5х2 у2 – 3х2 у => ху3 + 5х2 у2 – 3х2 у = ху3 + 5х2 у2 – 3х2 у => верно.2 b(а – 2b) = 3а2+1 b – 6а2 b1+1 = 3а3 b – 6а2 b2 => 3а3 b – 6а2 b2 = 3а3 b – 6а2 b2 => верно.2 х2 (3х – 2с + 1) = 6с2 х1+2 – 4с1+2 х2 + 2с2 х2 = 6с2 х3 – 4с3 х2 + 2с2 х2 => 6с2 х3 – 4с3 х2 + 2с2 х2 = 6с2 х3 – 4с3 х2 + 2с2 х2 => верно.
# 2.
1) а) х(а + с) – х(а + b) = х(а + с – (а + b)) = х(а + с – а – b) = х(с – b)2 (3а – 7с) – с2 (5а + 3с) = с2 (3а – 7с – (5а + 3с)) = с2 (3а – 7с – 5а – 3с) = с2 (–2а – 10с)
2) а) у(а + с) + х(а + с) = (а + с) (у + х)
3) а) а(b – с) + с(с – b) = а(b – с) – с(b – с) = (b – с)(а – с)
# 3.
а) Фигура состоит из двух полукругов и прямоугольника (два полукруга = круг).прямоуг = а • 2r, Sкруга = πr2 фигуры = Sпрямоуг + Sкруга = a • 2r + πr2 = r(2a + πr),
б) Фигура состоит из квадрата минус два полукруга (два полукруга = круг).квадрата = (2r)2 , Sкруга = πr2 Sфигуры = Sквадрата – Sкруга = (2r)2 – πr2 = 4r2 – πr2 = r2 (4 – π).
# 1.
1) а) 2x + 3xy = x(2 + 3y). Проверка: х(2 + 3у) = 2х + 3ху => 2х + 3ху = 2х + 3ху => верно.
2) а) Проверка: 5а(b + 2а) = 5ab + 10а1+1 => 5ab + 10а2 = 5ab + 10а2 => верно.2 – 7n => 14mn2 – 7n = 14mn2 – 7n => верно.1+1 + 80bс => –20с2 + 80bс = –20с2 + 80bс => верно.2 + 4у) = –3а2 у – 12у2 => –3a2 y – 12у2 = –3a2 y – 12у2 => верно.
3) а) а4 + а3 = а3 (а4–3 + 1) = а3 (а + 1). Проверка: а3 (а + 1) = а3+1 + а3 => а4 + а3 = а4 + а3 => верно.3 (z2 – 2) = 2z5 – 4z3 => 2z5 – 4z3 = 2z5 – 4z3 => верно.6 (3 + 7с – 8с2 ) = 3с6 + 7с1+6 – 8с2+6 = 3с6 + 7с7 – 8с8 => 3с6 + 7с7 – 8с8 = 3с6 + 7с7 – 8с8 => верно.2 (1 – 2х – 3х2 ) = 5х2 – 10х2+1 – 15х2+2 = 5х2 – 10х3 – 15х4 => 5х2 – 10х3 – 15х4 = 5х2 – 10х3 – 15х4 => верно.
4) а) ах2 + 3ах = ах(х2–1 + 3) = ах(х + 3). Проверка: ах(х + 3) = ах1+1 + 3ах = ах2 + 3ах => ах2 + 3ах = ах2 + 3ах => верно.2 + 5ху – 3х) = xy2+1 + 5х1+1 у1+1 – 3х1+1 у = ху3 + 5х2 у2 – 3х2 у => ху3 + 5х2 у2 – 3х2 у = ху3 + 5х2 у2 – 3х2 у => верно.2 b(а – 2b) = 3а2+1 b – 6а2 b1+1 = 3а3 b – 6а2 b2 => 3а3 b – 6а2 b2 = 3а3 b – 6а2 b2 => верно.2 х2 (3х – 2с + 1) = 6с2 х1+2 – 4с1+2 х2 + 2с2 х2 = 6с2 х3 – 4с3 х2 + 2с2 х2 => 6с2 х3 – 4с3 х2 + 2с2 х2 = 6с2 х3 – 4с3 х2 + 2с2 х2 => верно.
# 2.
1) а) х(а + с) – х(а + b) = х(а + с – (а + b)) = х(а + с – а – b) = х(с – b)2 (3а – 7с) – с2 (5а + 3с) = с2 (3а – 7с – (5а + 3с)) = с2 (3а – 7с – 5а – 3с) = с2 (–2а – 10с)
2) а) у(а + с) + х(а + с) = (а + с) (у + х)
3) а) а(b – с) + с(с – b) = а(b – с) – с(b – с) = (b – с)(а – с)
# 3.
а) Фигура состоит из двух полукругов и прямоугольника (два полукруга = круг).прямоуг = а • 2r, Sкруга = πr2 фигуры = Sпрямоуг + Sкруга = a • 2r + πr2 = r(2a + πr),
б) Фигура состоит из квадрата минус два полукруга (два полукруга = круг).квадрата = (2r)2 , Sкруга = πr2 Sфигуры = Sквадрата – Sкруга = (2r)2 – πr2 = 4r2 – πr2 = r2 (4 – π).
Вы смотрели : Самостоятельная работа по алгебре в 7 классе «Вынесение общего множителя за скобки» с ответами для УМК Макарычев Вариант 1 . Дидактические материалы для учителей, учащихся и родителей. Алгебра 7 Макарычев С-32 В1.
Другой вариант: С-32. Вариант 2
Вернуться на страницу: САМОСТОЯТЕЛЬНЫЕ работы по алгебре в 7 классе УМК Макарычев.
Перейти на страницу: КОНТРОЛЬНЫЕ работы по алгебре в 7 классе УМК Макарычев.
Цитаты (упражнения) из учебного пособия «Дидактические материалы. Алгебра 7 класс / Мерзляк, Полонский, Рабинович, Якир — М.:Вентана-Граф» использованы на сайте исключительно в учебных целях